Make your C# applications faster with LINQ joins

Modified August 15, 2022

Tim Deschryver

timdeschryver.dev

I've experienced a handful of times that an application has slowed down sufficiently without a code change. So, what could (change to) make an application slower over time? Mostly, the answer to this question is data. To be more specific, the amount of data that an application has to process.

During development, we as developers, often develop against a small subset of the data. This has as outcome, that parts of an application seem fast during this stage. And when it reaches the production environment it still is fast. But after a while, when the application is in use, the data starts to accumulate and it might suddenly be the cause of performance issues.

From my experience, most of these performance problems are caused while combining two lists in order to manipulate the data. And don't get me wrong, it's an easy mistake.

The slow approach link

As an example, let's take two lists, one with the customers, the second one with the customer preferences. We want to merge the two lists into a single list, representing the customer data with their preference.

How many times did you write or encounter the following code?

 Foreach-loop content_paste
var customersWithPreference = new List<CustomerAggregate>();
foreach (var customer in customers)
{
  var preference = customersPreference.SingleOrDefault(preference => preference.CustomerId == customer.Id);
  customersWithPreference.Add(new CustomerAggregate
  {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference
  });
}

Another commonly approach is to write it with the LINQ Select method.

 LINQ Select content_paste
var customersWithPreference = customers.Select(customer => {
  var preference = customersPreference.SingleOrDefault(preference => preference.CustomerId == customer.Id);
  return new CustomerAggregate {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference
  };
});

Well... then I got bad news for you because this isn't fast for larger lists.

The faster approach link

But how should this be written then? A better approach with performance in mind is to use the LINQ Join method.

 LINQ method Join content_paste
var customersWithPreference = customers.Join(
  customersPreference,
  customer => customer.Id,
  preference => preference.CustomerId,
  (customer, preference) => new CustomerAggregate
  {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference
  });

If you're more a fan of the LINQ query syntax, then the above snippet can be rewritten to:

 LINQ query Join content_paste
var customersWithPreference =
  from customer in customers
  join preference in customersPreference on customer.Id equals preference.CustomerId
  select new CustomerAggregate
  {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference
  };

Both of the LINQ examples don't only perform better, but they also make the intentions more clear in my opinion.

Why it does perform better link

As pointed on out in a reddit thread, it isn't LINQ that's making this faster.

The cause of these improvements is found in the lookup of the Join method, not LINQ itself. To prove that LINQ does, in fact, make things actually a tiny bit slower can be tested with the following code.

 Dictionary content_paste
var customersPreferenceDict = customersPreferences.ToDictionary(k => k.CustomerId);
var customersWithPreference = customers.Select(customer =>
{
  var preference = customersPreferenceDict[customer.Id];
  return new CustomerAggregate
  {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference
  };
})

 Manual iteration content_paste
var preferences = new Dictionary<int, CustomerPreference>(customersPreferences.Length);
foreach (var p in customersPreferences)
{
  preferences.Add(p.CustomerId, p);
}
 
customerAggregates = new List<CustomerAggregate>(customers.Length);
foreach (var customer in customers)
{
  preferences.TryGetValue(customer.Id, out var preference);
  customerAggregates.Add(new CustomerAggregate
  {
    CustomerId = customer.Id,
    Name = customer.Name,
    Preference = preference,
  });
}

Benchmarks link

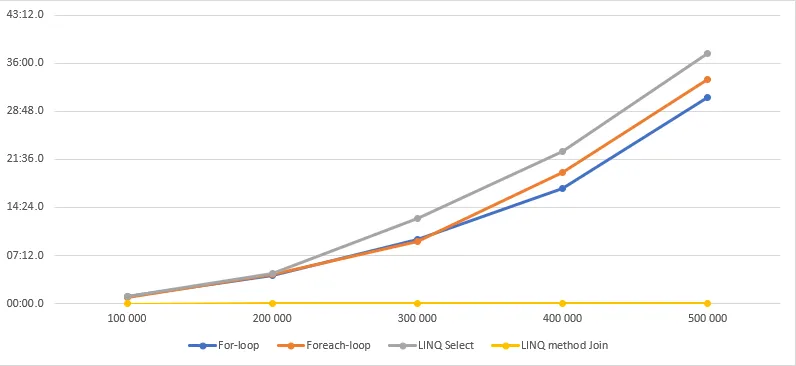
You don't have to take my word for it, here's a comparison of all the methods that are described in this post. On my machine, this gives us the following result.

format_quote

Benchmarks are created with Simple microbenchmarking in C#

I expected the LINQ examples to be faster, but I was still surprised by the margins of these results.

To play with the solutions yourselves, here's a link to the GitHub repository with the examples included.

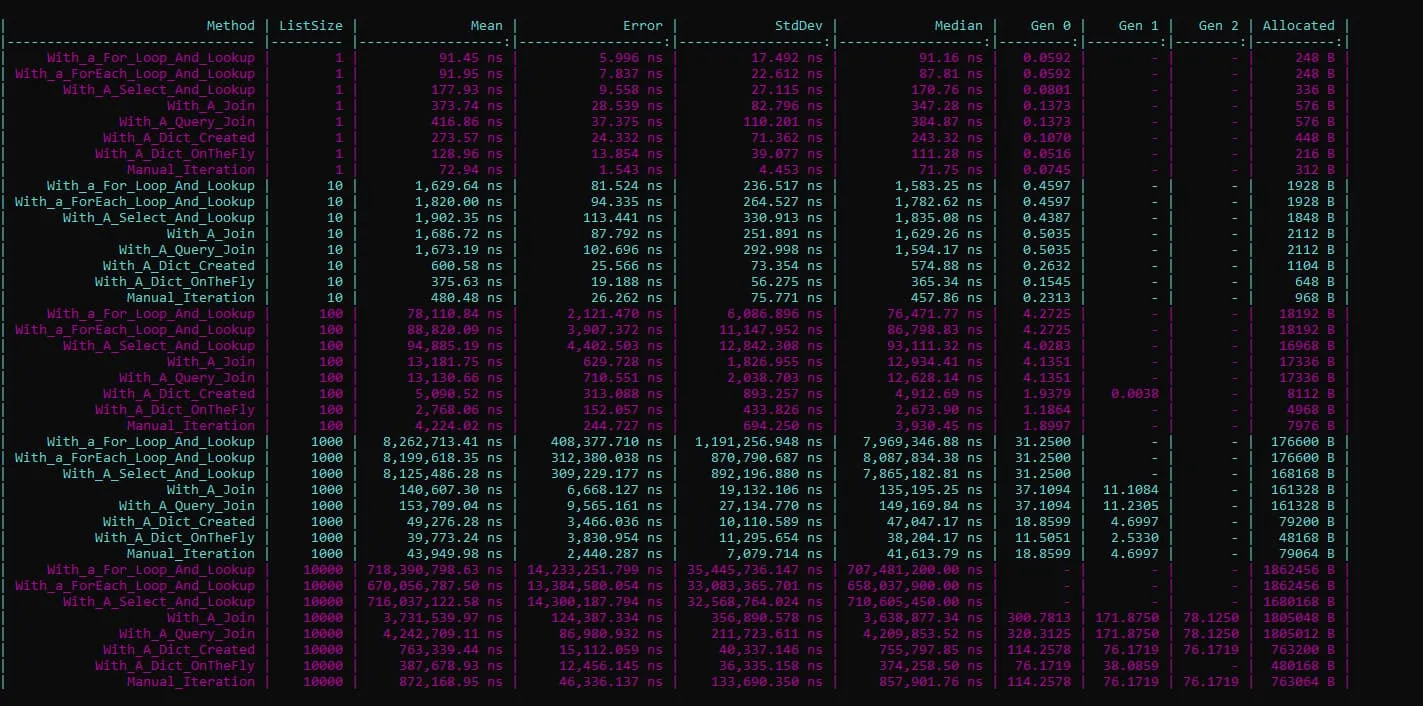
Thanks to a community contribution, these benchmarks are also created with BenchmarkDotNet and gives us the following results:

Conclusion link

The reason why the numbers ramp up is that at its worst-case scenario, it has to traverse through the whole list until the predicate finds a match. The larger the list gets, the slower the code will run. We can express this algorithm with the Big O Notation as O(N), which describes a linear growth in proportion to the size of the list.

To do better we can make rewrite this to an O(1) algorithm, to make this lookup a single operation. Regardless of the size of the list.

Feel free to update this blog post on GitHub, thanks in advance!

Support me

I appreciate it if you would support me if have you enjoyed this post and found it useful, thank you in advance.

Share this post